Times flies and now we are in week 2 trying to write a pathtracer in Lua. Please check out Week 1 for high-level project overview, thoughts on C++/Lua interoperation, and more. This week, we will first implement model loading in C++, wrap it up into Lua, then use that model loading function to trace some cubes. Let’s go!

Model Loading

We will first make a simple scene class Model to represent the scene:

struct Vertex {
    glm::vec3 position;
    glm::vec3 normal;
    glm::vec2 tex_coord;
};

struct Triangle {
    Vertex a, b, c;
};

/**
 * The scene representation (for now.)
 */
class Model
{
public:
    /**
     * Default constructor
     */
    Model();

    /**
     * No copy constructor.
     */
    Model(const Model& other) = delete;

    /**
     * Destructor
     */
    ~Model();

    int id() const;

    bool load(const std::string &path, const std::string &mtl_base_dir = "");

    int get_num_verts() const;
    int get_num_tris() const;
    std::string get_load_warnings() const;
    std::string get_load_errors() const;

    const Triangle &get_triangle(int index) const;

private:
    int id_;
    bool initialized;
    std::vector<Triangle> tri;
    std::string load_warnings, load_errors;
};

The scene is made of triangles and for simplicity’s (laziness) sake, we will only support triangular meshes. The load method loads in the scene using tinyobjloader. It’s such a cool & fast library. If you want to learn more about it, I have written a blog post on using tinyobjloader as well.

As we can see right now not a lot is going on. There’s no support for light emitters, BRDFs, etc. Just triangles stored in memory. We will expand this class in the future but as of right now, those are what we have.

After implementing the methods in Model, we wrap them up so that they become Lua functions. For example:

int Lua::make_model(lua_State *l)
{
    const char *path = lua_tostring(l, 1);

    std::shared_ptr<Model> model = std::make_shared<Model>();
    if (!model->load(path))
    {
        luaL_error(l, "Cannot load model: %s", model->get_load_errors().c_str());
        return 0;
    }

    std::string warnings = model->get_load_warnings();
    if (!warnings.empty())
    {
        std::cerr << "WARNING! " << warnings << std::endl;
    }

    inst()->models.push_back(model);
    lua_pushinteger(l, model->id());
    return 1;
}

The craziest one to wrap so far is the Triangle::get_triangle function, as it requires returning 24 whole numbers:

int Lua::model_get_tri(lua_State *l)
{
    int id = lua_tointeger(l, 1);
    int index = lua_tointeger(l, 2);

    auto it = // locate triangle using id

    const Triangle &tri = (*it)->get_triangle(index);
    if (index < 0 || index >= (*it)->get_num_tris())
    {
        luaL_error(l, "Triangle index out of bounds: %d.", index);
        return 0;
    }

    lua_pushnumber(l, tri.a.position.x);
    lua_pushnumber(l, tri.a.position.y);
    lua_pushnumber(l, tri.a.position.z);
    lua_pushnumber(l, tri.a.normal.x);
    // ... this goes on for a while

And now we move onto the Lua side. The premise is basically the same to the Image we mentioned in the previous post. After defining a __gc function for Lua, Lua will now automagically frees the model after it becomes stale.

Model = {
    handle = 0,
    path = "",
    __gc = function()
        free_model(self.handle)
    end
}

function Model:new(path)
    local ret = {}
    setmetatable(ret, self)
    self.__index = self
    ret.path = path
    ret.handle = make_model(path)
    return ret
end

function Model:tri_count()
    return model_tri_count(self.handle)
end

function Model:tri(index)
    local apx, apy, apz, anx, any, anz, au, av, bpx, bpy, bpz, bnx, bny, bnz, bu, bv, cpx, cpy, cpz, cnx, cny, cnz, cu, cv = model_get_tri(self.handle, index - 1)

    local tri = Triangle:new()
    tri.a:set(Vec4:new(apx, apy, apz, 1.0), Vec4:new(anx, any, anz, 1.0), Vec4:new(au, av))
    tri.b:set(Vec4:new(bpx, bpy, bpz, 1.0), Vec4:new(bnx, bny, bnz, 1.0), Vec4:new(bu, bv))
    tri.c:set(Vec4:new(cpx, cpy, cpz, 1.0), Vec4:new(cnx, cny, cnz, 1.0), Vec4:new(cu, cv))

    return tri
end

The tri function constructs a triangle defined in Lua by using the 24 values the model_get_tri function returned above. I am not too sure about this as the performance might be abysmal (because this will be called MANY times for MANY pixels) but I can think of no better alternatives so far.

With the above wrapping done, we can now load & manipulate the scene entirely in Lua.

Intersection

Since the whole scene is now accessible in Lua, we can implement the most important thing for any raytracers/pathtracers - the intersection function. The main intersection function I am going for here is the ray-triangle intersection function, as we will only support triangular meshes.

There are many ways to do a ray-triangle intersection, and a lot of excellent online resources are available. If you are interested, I would recommend the article in the Graphics Codex, CMU 15462, and the PBRT book. Here I will use a crude method, which is not particularly quick or efficient, but is kind of intuitive, and gets the job done.

Ray-plane Intersection

Before knowing whether there is a ray-triangle intersection, we have to know first if the ray intersects with the bounding plane of the triangle. We do this by performing a ray-plane intersection. A plane is defined by

where \(N\) is the normal direction of the plane. For a flat-shaded triangle, that means just about the normal direction of any of its three vertices. Our ray is define by

So assuming the ray does intersects with the plane, there exists a \(t_0\) which satisfies the \(N^T r(t_0) = c\).

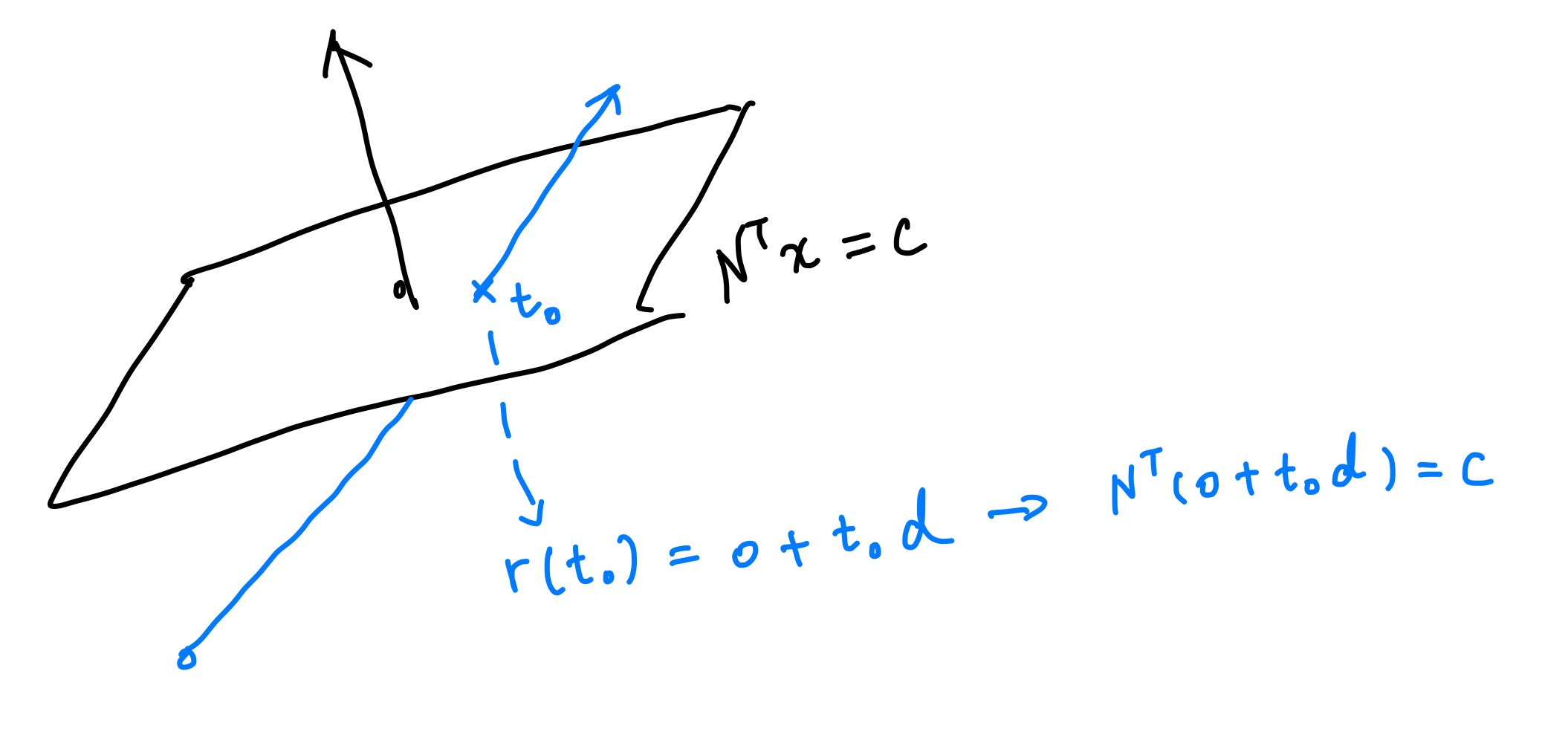
If we expand it and solve for \(t_0\) we get

This also means that when ray direction d is parallel to normal N, the intersection will be at the infinite point - and therefore there won’t be an intersection.

Our intersect function is defined as such. It accepts a ray origin, a ray direction, and a triangle. We also need to specify tmin and tmax so the intersection result won’t be way too far from us and won’t be behind the ray origin.

function intersect(ro, rd, tri, tmin, tmax)

First, we plug the position and the normal of a random point on the triangle in, and solve for c:

local c = tri.a.position:dot3(tri.a.normal)

After that, we just Lua-ify the above equation.

-- <N^T, d>
-- if the value is less than some threshold, we assume rd is parallel to N and therefore won't have an intersection
local ntd = tri.a.normal:dot3(rd)
if math.abs(ntd) < 0.001 then
    return nil
end

local t = (c - tri.a.normal:dot3(ro)) / ntd
if t < tmin or t > tmax then
    return nil
end

When a suitable t is found, that means now we also have the intersected point on the plane (\(p_0 = o + t_0 d\)).

Ray-triangle Intersection

Now onto determining whether the point is inside the triangle. We do this by calculating the barycentric coordinate of point \(p_0\). In simple terms, barycentric coordinates are related to the areas of the small triangles that are formed when point \(p_0\) is inside a triangle. To determine if there’s an intersection, we first calculate the ratios of these small triangles’ areas to the entire triangle’s area. Then we confirm that:

1. The sum of these ratios, which correspond to the barycentric coordinates, is equal to 1;
2. None of these ratios are greather than 1.

If any of them fails, then there is no intersection.

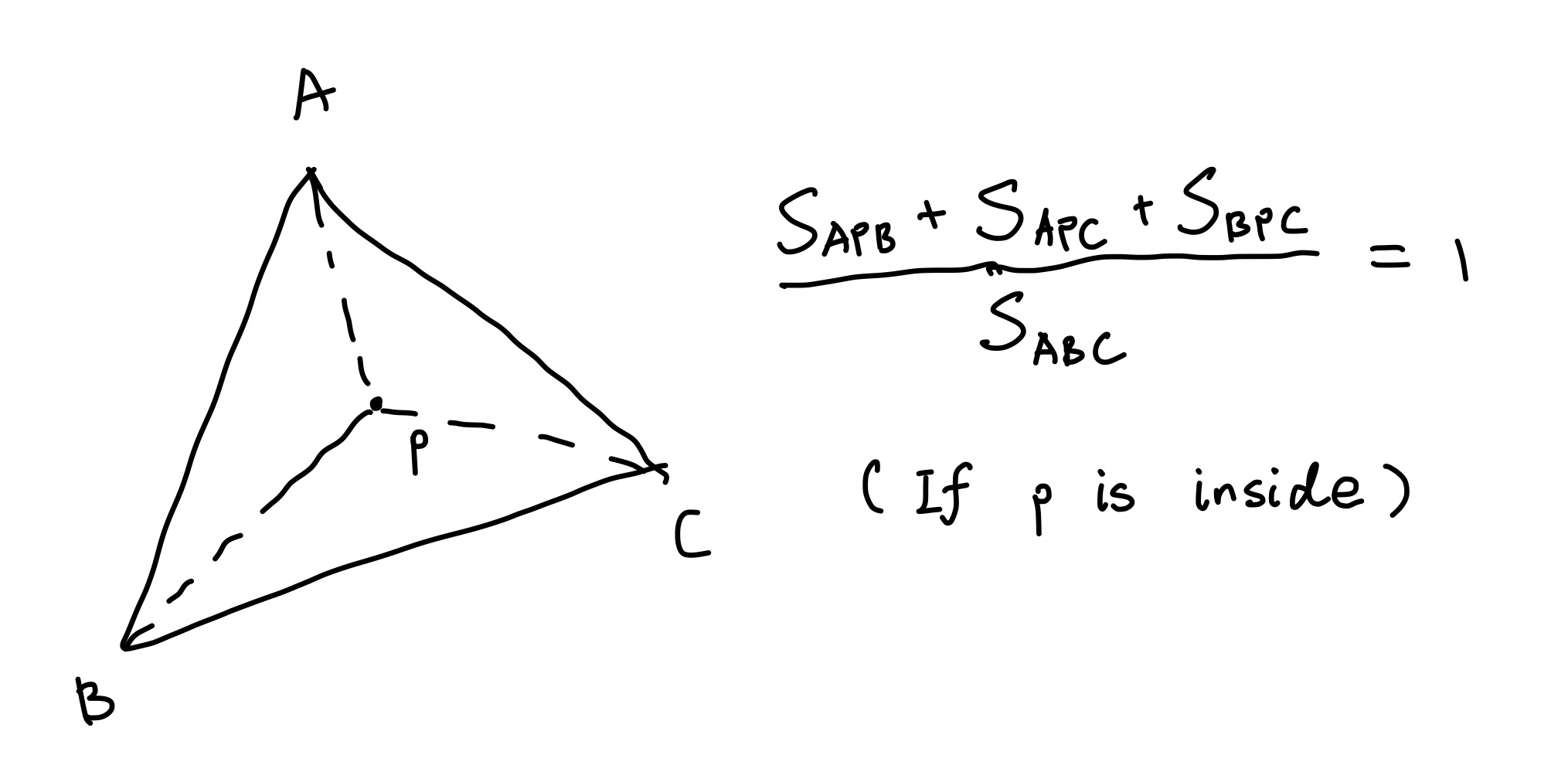
We calculate the triangle area by using the length of the cross product of any of the two vectors formed by any verties in a triangle, for the length of the cross product is the area of the corressponding parallelogram:

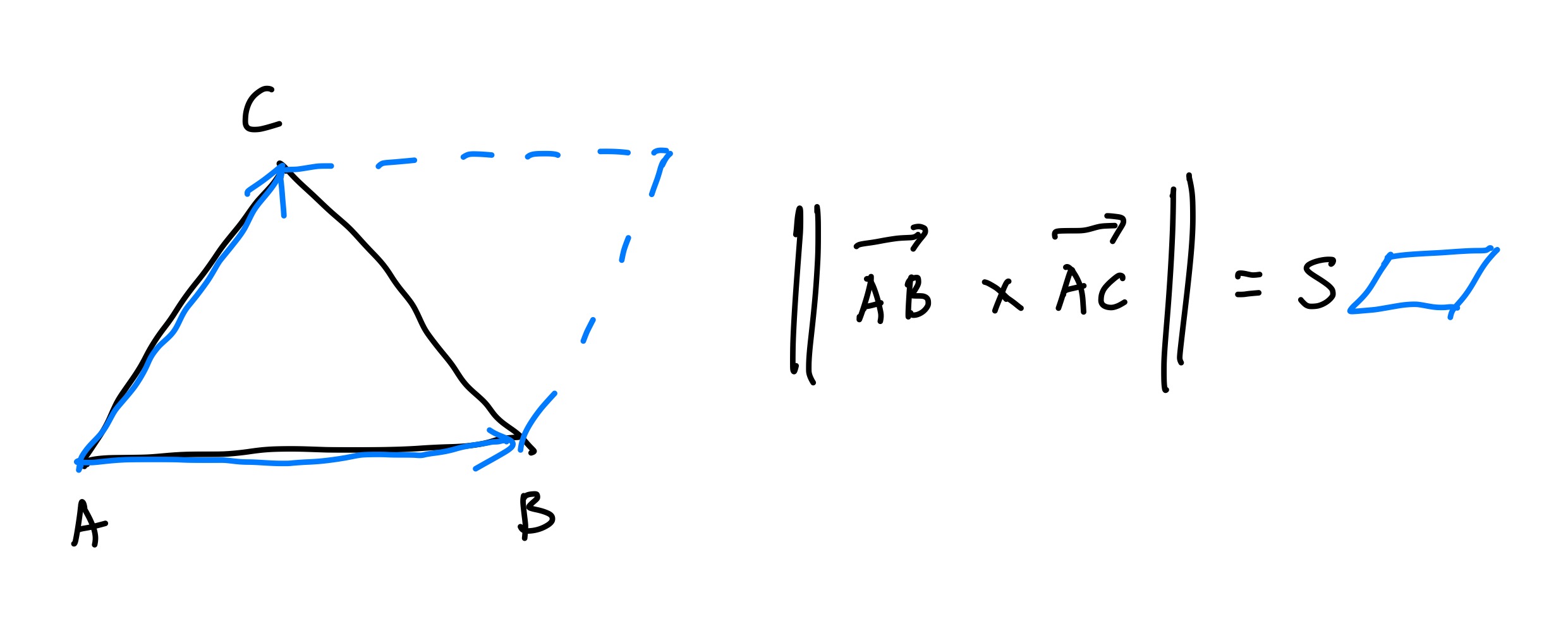
Here’s the whole shebang in Lua:

-- ... continued from above

local p = ro:add(rd:scl(t))

-- If there's an intersection, try to figure out the barycentric coordinate to check whether it's in the triangle or not
local ab = tri.b.position:subtr(tri.a.position)
local ac = tri.c.position:subtr(tri.a.position)
local sabc = ab:cross(ac):len3() / 2

local ap = p:subtr(tri.a.position)
local cb = tri.b.position:subtr(tri.c.position)
local cp = p:subtr(tri.c.position)
local u = (ab:cross(ap):len3() / 2) / sabc
local v = (ap:cross(ac):len3() / 2) / sabc
local w = (cp:cross(cb):len3() / 2) / sabc

if u < 0 or v < 0 or w < 0 or u > 1 or v > 1 or w > 1 or math.abs(u + v + w - 1) > 0.01 then
    return nil
end

return t

Current Result

With the most crucial part of ray tracing done, now we can actually trace some rays. We can even shade the result because we have normals in hand.

require "lib/image"
require "lib/model"
require "math"
local pprint = require "lib/pprint"

local size = 100
local im = Image:new(size, size)
local model = Model:new("cube.obj")
print("Model loaded. #triangles:", model:tri_count())

function shade(u, v, x, y)
    local ro = Vec4:new(2, 1.2, 2.5, 1)
    local center = Vec4:new(0, 0.0, 0.0, 1)
    local front = center:subtr(ro):nor3() -- most of the time we won't be needing the 4th component
    local right = front:cross(Vec4:new(0, 1, 0, 1)):nor3()
    local up = right:cross(front):nor3()

    local rd = right:scl(u):add(up:scl(v)):add(front:scl(2)):nor3()

    -- keep record of the closest intersected triangle.
    local closest_tri = nil
    local closest_t = -1

    -- iterate through all triangles in the scene.
    for i = 1, model:tri_count() do
        local tri = model:tri(i)
        local t = intersect(ro, rd, tri, 0.01, 100.0)

        -- replace the triangle with the closest intersected.
        if t ~= nil and (t < closest_t or closest_tri == nil) then
            closest_tri = tri
            closest_t = t
        end
    end

    if closest_tri == nil then
        -- color background
        local uu = math.floor(u * 5)
        local vv = math.floor(v * 5)
        if (uu + vv) % 2 == 0 then
            return Vec4:new(0.1, 0.1, 0.1, 1)
        else
            return Vec4:new(0.9, 0.9, 0.9, 1)
        end
    end

    -- shade the intersected triangle.
    local rd = Vec4:new(1, 0.5, 0.2, 1):nor3()
    local ambient = 0.2
    local diffuse = math.max(0, rd:dot3(closest_tri.a.normal))

    return Vec4:new(1.0, 0.5, 0.0, 1):scl(ambient + diffuse)
end

for y = 1, size do
    for x = 1, size do
        u = (x - 1) / size * 2.0 - 1.0
        v = (y - 1) / size * 2.0 - 1.0
        res = shade(u, v, x - 1, y - 1)
        im:pixel_vec4(x - 1, y - 1, res)
    end
end

im:save("cube.png")

How about a torus?

Or, dare I try it, Suzanne?

Conclusion

Different .obj files can now be traced by changing just one line and running the Lua script again, with no need for recompilation. This is very cool and is also a big part of why I want to do this in Lua - soon we will be needing to debug a large amount of graphics code, and graphics code are very, very hard to debug. However when the whole thing’s in Lua, we can iterate & debug extremely fast, by running the same patch of code over and over again, with little to no down time waiting for the project to recompile. We can also just change one line of code to see the change in render result. And on top of it all, it’s just very cool.

However, the limitation of Lua is starting to show. A simple 100x100 raytrace takes quite some time - the cube needs at least 10 seconds, the torus 60, and the monkey took like 90 seconds or so. With each new triangle the complexity to trace the scene will definitely explode, not to mention we didn’t even start solving the rendering equation yet. BVH and multithreading should be implemented sooner or later or the whole thing will become unusable.

There’s another problem in the intersect code presented above. This only works for flat-shaded meshes where each vertex of a face has the same normals - smooth shaded mesh’s normals will vary, making the above code janky. One way to solve this is to calculate real normals on the fly, or use another intersection algorithm. I guess I’ll see what I can do. So as always, stay tuned for more!

Comments

A valid, non-empty username is required.

Comment