- Week 1: project introduction and high-level design
- Week 2: model loading & intersection
- Week 3: rudimentary UI and job dispatch system
- Week 4: true multithreaded Lua)
- Week 5 (you are here)
Hi! This week marks a great change for LuaPT. To further accelerate the tracing process, multiple things have been optimized and changed, and some are rebuilt from the ground up. This week, we will be introducing LuaJIT, and most importantly, the ffi extension. After that, we will implement a BVH acceleration structure in full Lua (or at least 80% Lua). LuaJIT has accelerated Lua so much and ffi has greatly simplified C++/Lua interoperation, I don’t even know where to begin. So let’s begin!

LuaJIT
I have started trying improving the speed of LuaPT since week 4. Since week 3 begins LuaPT’s performance has been rapidly degrading and I know that soon enough, it will be so slow that I might as well trace the rays by hand. But this is when LuaJIT comes to the rescue. By simply replacing my exisitng Lua library and linking LuaJIT instead I can already see a significant increase in speed.
Next, by using ffi extension I ported my whole math library to C++.
As models & meshes are represented using a continuous glm::vec3 vector, we can exploit this fact and force a pointer cast when the Lua script is asking for triangles. Vector math in C++ is magnitudes faster than in Lua, and by doing so I achieved another speed up.
The ffi library is so cool. I just need to implement the functions in C++ (with an extern C block), then copy & paste my header into a ffi.cdef block. Now I can just call these functions in Lua. It’s crazy how convenient it is.
The switch to LuaJIT is time-consuming but nothing too technical. All the previous methods and APIs (including Image and Model) ported onto LuaJIT, however losing their object-oriented APIs in the process. But I think it’s a rather small sacrifice to obtain the Speed. If you are interested in learning how LuaJIT works, I strongly recommend you check out the official website. It’s short, concise, and in less than 10 lines of code showed me how I can use it. It’s awesome. So after deprecating the Lua library and switching to LuaJIT, I begin working on a few other improvements.
Intersection
Ray-Box Intersection
As we will be implementing a BVH, we have to implement a ray-box intersection method first. Here we will make use of the one in Scratchapixel, aka the slab method.
function intersect_box(ro, rd, box)
local rdinv = vec3(1 / rd.x, 1 / rd.y, 1 / rd.z)
local tmin = -1e309 -- 1e309 is infinity in Lua
local tmax = 1e309
if rd.x ~= 0 then
local tx1 = (box.min.x - ro.x) * rdinv.x
local tx2 = (box.max.x - ro.x) * rdinv.x
tmin = math.max(tmin, math.min(tx1, tx2))
tmax = math.min(tmax, math.max(tx1, tx2))
end
if rd.y ~= 0 then
local ty1 = (box.min.y - ro.y) * rdinv.y
local ty2 = (box.max.y - ro.y) * rdinv.y
tmin = math.max(tmin, math.min(ty1, ty2))
tmax = math.min(tmax, math.max(ty1, ty2))
end
if rd.z ~= 0 then
local tz1 = (box.min.z - ro.z) * rdinv.z
local tz2 = (box.max.z - ro.z) * rdinv.z
tmin = math.max(tmin, math.min(tz1, tz2))
tmax = math.min(tmax, math.max(tz1, tz2))
end
if tmax >= tmin then
return tmin, tmax
else
return nil
end
end
Of course then we will need a bounding box data structure. The bounding box BBox is first defined in plain C then passed onto Lua using LuaJIT.
typedef struct
{
Vec3C min, max;
} BBox;
Better Ray-Triangle Intersection
The brute force method of ray-triangle intersection test introduced in week 2 is also starting to slow us down. To counter this issue, I have switched the ray-triangle intersection test to a faster one, namely the Moller-Trumbore method. both the Scotty3D website and Scratchapixel are excellent learning sources.
function intersect_mt(ro, rd, tri, tmin, tmax)
local e1 = sub3(tri.b.position, tri.a.position)
local e2 = sub3(tri.c.position, tri.a.position)
local pvec = cross(rd, e2)
local det = dot3(e1, pvec)
-- Are they almost parallel?
if (math.abs(det) < 0.0001) then
return nil
end
local inv = 1.0 / det
local tvec = sub3(ro, tri.a.position)
local u = dot3(pvec, tvec) * inv
if u < 0 or u > 1 then
return nil
end
local qvec = cross(tvec, e1)
local v = dot3(rd, qvec) * inv
if v < 0 or u + v > 1 then
return nil
end
local t = dot3(e2, qvec) * inv
if t < tmin or t > tmax then
return nil
end
return vec3(u, v, t)
end
To further increase render precision, add more zeros to if (math.abs(det) < 0.0001) then. The implementation of Moller-Trumbore method gave us a slight speed increase for each pixel.
BVH Construction
And finally, now it’s time for us to construct a BVH. We can’t implement the whole BVH in Lua, because multithreading is achieved through multiple Lua instances and there isn’t an effective way to sync Lua variables between Lua states. So instead, the BVH data structure will be defined in C/C++, with a few getters/setters, but no serious functions that could construct a BVH directly.
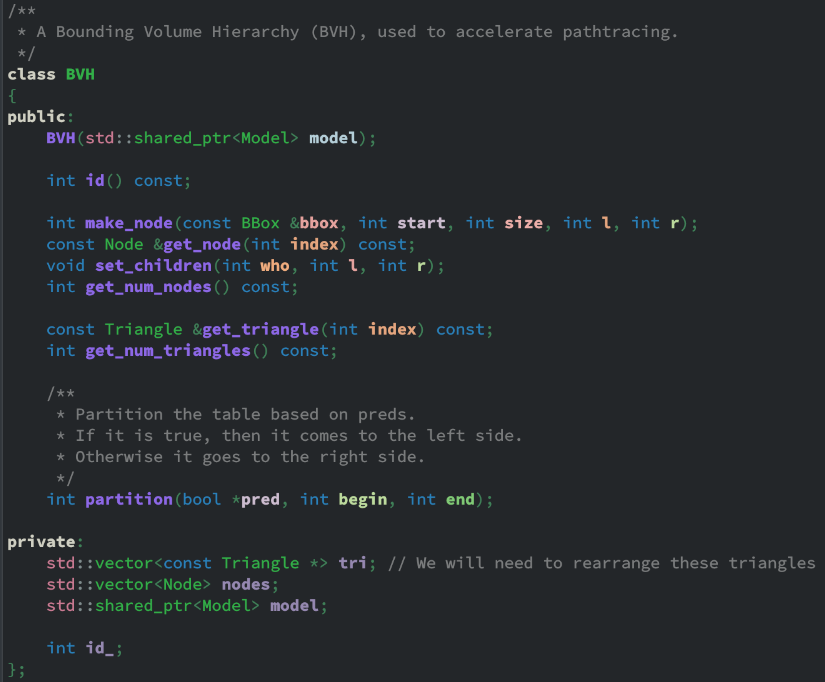
BVH Definition (C++ Part)
The only notable functions are the constructor of BVH and the partition function. We will go over them one by one. In BVH::BVH, we accept a pointer to a Model. The BVH class then copies all triangles into its own array, and creates a root node in the nodes variable. The nodes variable acts like a complete binary tree stored in continuous memory. You can think of it as a heap.
BVH::BVH(std::shared_ptr<Model> model) : model(model)
{
// First make an empty node to fit ALL triangles inside
BBox root_bbox = bbox();
for (int i = 0; i < model->get_num_tris(); i++)
{
TriC *t = model_get_tri(model.get(), i);
// The enclose method encloses a point into a bounding box
enclose(root_bbox, t->a.position);
enclose(root_bbox, t->b.position);
enclose(root_bbox, t->c.position);
tri.push_back(&model->get_triangle(i));
}
make_node(root_bbox, 0, tri.size(), 0, 0);
}
The make_node method is just that - it makes a node, pushes it onto nodes, and return its index. The node is defined as such:
typedef struct
{
BBox bbox;
int start, size;
int l, r; // Left child & right child
} Node;
In this case, we construct a root node for our BVH, make it contain the full triangle array (0 to tri.size()), and its bounding box enclosing all the vertices of the input mesh.
Because BVH stores triangles in whatever order the input mesh give us, we will need some way to rearrange the order of triangles. And to stay true to our project name, Lua has to be the one who does the job. std::partition therefore is out of the question - its final parameter pred requires a lambda function in C/C++. We therefore have to resort to a homemade partition method. By accepting an array of booleans, and putting the true values to the left, false values to the right, we can partition basically anything coming from Lua, with just an extra smidge of memory cost.
int BVH::partition(bool *pred, int begin, int end)
{
assert(begin >= 0 && end < tri.size() && "Invalid partition range");
while (begin <= end)
{
if (!pred[begin])
{
const Triangle *t = tri[begin];
tri[begin] = tri[end];
tri[end] = t;
// Gotta swap that pred as well
bool p = pred[begin];
pred[begin] = pred[end];
pred[end] = p;
end--;
}
else
{
begin++;
}
}
return begin;
}
BVH Construction (Lua Part)
That’s the whole of C++ part. As you can see, not a lot is going on in there. The real interesting thing happens in Lua.
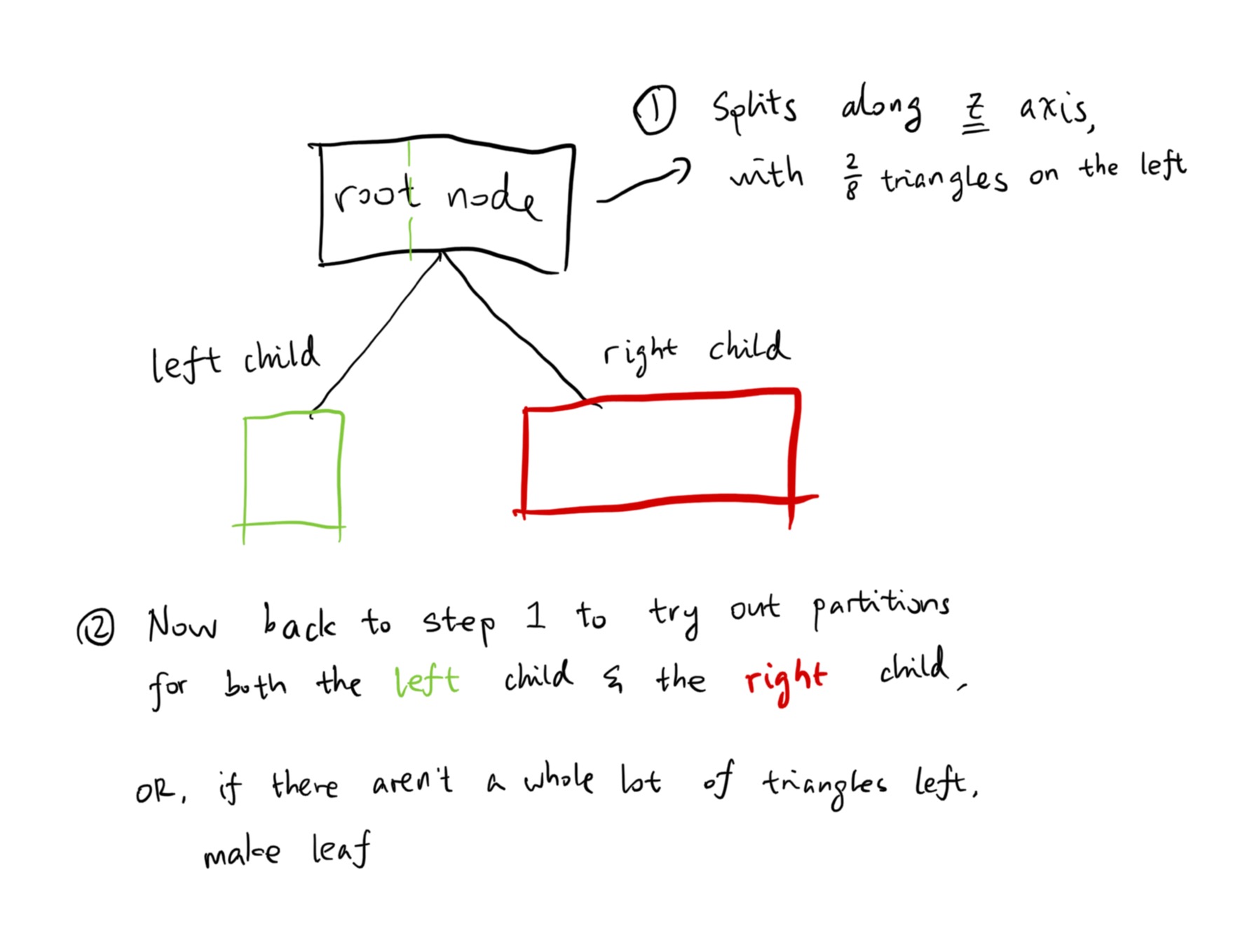
- The current (root) node and its bounding box is obtained via the Lua ffi API.
- For each axis, 8 valid partitions among the bounding box domain is tried.
- A “Surface Area Heuristic” (SAH) is evaluated for each partition along each domain, and the best one with the lowest score is kept.
- Finally revert all the changes and execute the partition method with the best SAH.
- The mesh is now split into 2 following the partition; make 2 new nodes and for each of them, either make leaf or continue partitioning (back to step 1).
Demonstrated below. First, we find the perfect partition with the lowest SAH score:
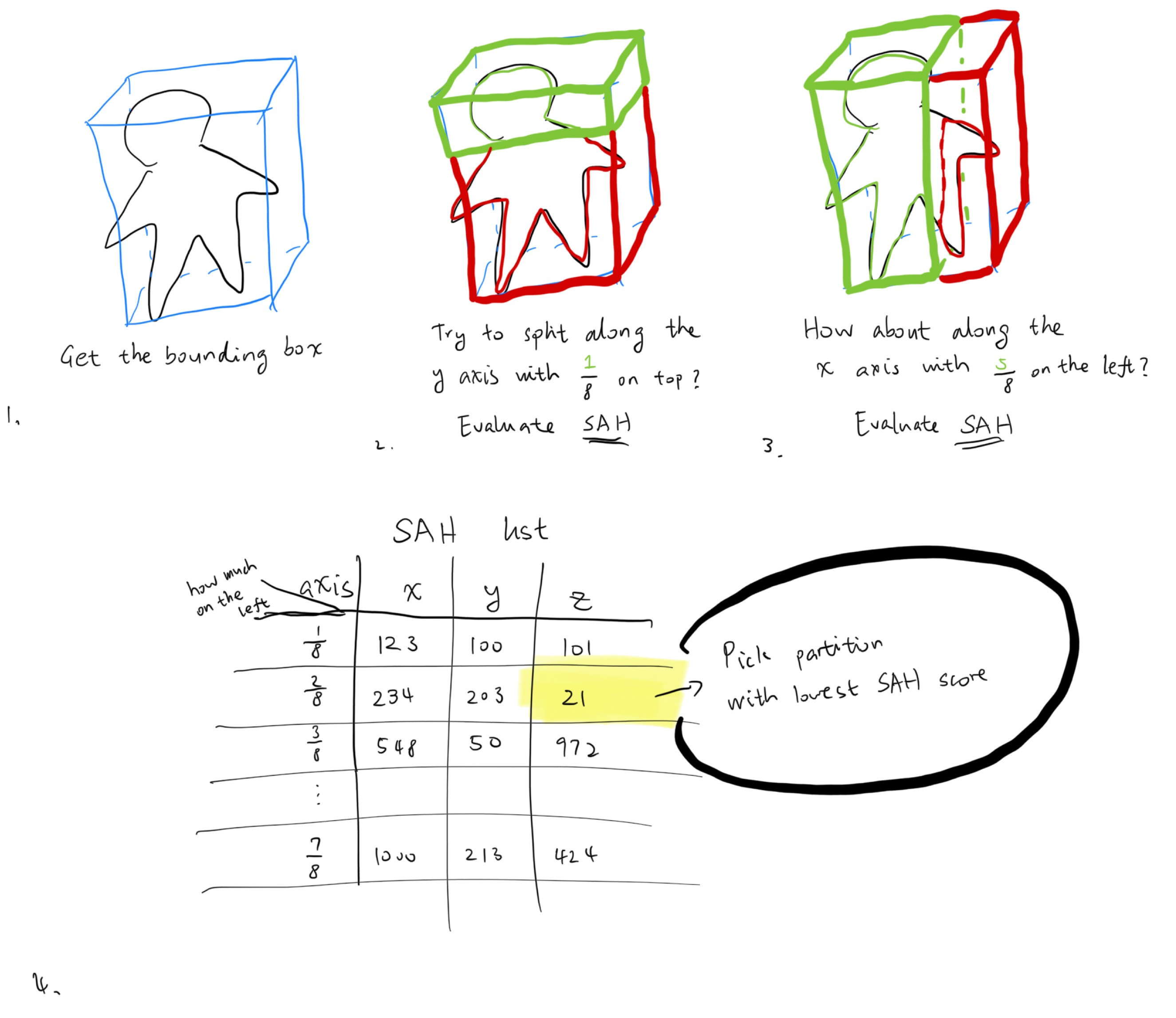
Then, we partition the triangles within the node accordingly. Then, we split the array and give them to two new children, and recurse to obtain the best partition for them. This goes on until there aren’t enough triangles to partition, or the best partition is no partition. Then we stop.
For us, the SAH equation is
\[\text{SAH} = C_\text{trav} + \frac{S_\text{left}}{S} N_\text{left} C_\text{isect} + \frac{S_\text{right}}{S} N_\text{right} C_\text{isect}\]In which \(C_\text{trav}\) (the travel cost) is a constant of 1 and the intersect cost \(C_\text{isect}\) is 2. The \(\frac{S_\text{left}}{S}\) and \(\frac{S_\text{right}}{S}\) are simply the split ratio (the \(\frac{k}{8}\) above).
This is how that looks in Lua:
-- First call the BVH constructor with a model
local bvh = make_bvh(model)
function determine_side(p, offset, axis)
if axis == 0 then
return p.x < offset.x
elseif axis == 1 then
return p.y < offset.y
else
return p.z < offset.z
end
end
function determine_area_ratio(poff, span, axis)
if axis == 0 then
return poff.x / span.x, (span.x - poff.x) / span.x
elseif axis == 1 then
return poff.y / span.y, (span.y - poff.y) / span.y
else
return poff.z / span.z, (span.z - poff.z) / span.z
end
end
function bvh_construct(node_idx, start, fin)
if fin - start + 1 <= 8 then
-- No need to make BVH; not a lot of triangles here
return
end
local n = bvh_get_node(bvh, node_idx)
local span = sub3(n.bbox.max, n.bbox.min)
-- split them into 8 buckets
local num_buckets = 8
local split_step = scl3(span, 1 / num_buckets)
-- Bests
local best_axis = 0
local best_step = 1
local best_sah = 1e309
local best_offset = 0
for axis = 0, 2 do
-- Tentatively partition them along these axis
for step = 1, 7 do
-- 1. Somehow partition it.
local table = make_partitioning_table(bvh)
local poff = scl3(split_step, step) -- Plane offset
local plane = add3(n.bbox.min, poff)
for i = start, fin do
local tri = bvh_get_tri(bvh, i)
local centroid = scl3(add3(add3(tri.a.position, tri.b.position), tri.c.position), 1 / 3)
table[i] = determine_side(centroid, plane, axis)
end
local offset = partition(bvh, table, start, fin)
-- 2. Calculate SAH. Record the best one.
local left, right = determine_area_ratio(poff, span, axis)
local sah = 1 + 2 * left * (offset - start) + 2 * right * (fin - offset + 1)
if sah < best_sah then
best_sah = sah
best_step = step
best_axis = axis
best_offset = offset
end
end
end
-- That's not very constructive.
if best_offset == start or best_offset == fin + 1 then
return
end
-- Partition using the best one.
local table = make_partitioning_table(bvh)
local poff = scl3(split_step, best_step)
local plane = add3(n.bbox.min, poff)
for i = start, fin do
local tri = bvh_get_tri(bvh, i)
local centroid = scl3(add3(add3(tri.a.position, tri.b.position), tri.c.position), 1 / 3)
table[i] = determine_side(centroid, plane, best_axis)
end
local offset = partition(bvh, table, start, fin)
local left_box = bbox()
local right_box = bbox()
for i = start, offset - 1 do
local tri = bvh_get_tri(bvh, i)
enclose(left_box, tri.a.position)
enclose(left_box, tri.b.position)
enclose(left_box, tri.c.position)
end
for i = offset, fin do
local tri = bvh_get_tri(bvh, i)
enclose(right_box, tri.a.position)
enclose(right_box, tri.b.position)
enclose(right_box, tri.c.position)
end
local l = bvh_push_node(bvh, left_box, start, offset - start, 0, 0)
local r = bvh_push_node(bvh, right_box, offset, fin - offset + 1, 0, 0)
bvh_node_set_children(bvh, node_idx, l, r)
-- Recurse into l and r ???
bvh_construct(l, start, offset - 1)
bvh_construct(r, offset, fin)
end
-- Construct BVH for the whole thing
bvh_construct(0, 0, bvh_tri_count(bvh) - 1)
Current Result
With the shiny new BVH in place, combined with LuaJIT, our render is now much, much faster. Compared to a non-BVH (yes-LuaJIT) rendering of Spot the cow, which can take up to 10 minute, BVH-enabled version of the same scene now only takes 2 and a half minutes.

Here’s the Blender monkey Suzanne:

Aaaand here’s a 720p torus.

If you have you missed it, here’s the link to the source code. Hit a star if you feel like it. It will always shoot a stream of dopamine straight to my brain. But in any case, I will see you next week!
Further Readings
- LuaJIT, the Just-in-Time Lua compiler
- LuaJIT ffi, the ffi extension documentation
- Ray-Box Intersection, Scratchapixel)
- Moller-Trumbore Fast Ray-Triangle Intersection, Wikipedia
- Surface Area Heuristic (SAH), CMU 15462/662
- Fast, Branchless Ray/Bounding Box Intersections
- How to create awesome accelerators: The Surface Area Heuristic
Comments